Математика/5. Математическое моделирование
К.п.н., Чернобровкина И.И.
Орловский государственный университет, Россия
Метод оценки уровня устойчивости нейронно-сетевых
регрессионных моделей
Проблема оценки устойчивости нейронных сетей не нова и на сегодняшний
день имеются различные подходы к ее решению [1, 2, 3, 4]. Для того, чтобы
построенная нейронно-сетевая модель могла быть успешно применима на практике,
необходимо проверить ее на устойчивость. Модель считается устойчивой, если малым
изменениям входных параметров отвечают малые изменения выходного параметра.
Одним из наиболее широких направлений
применения нейронных сетей в экономико-математическом моделировании является
построение регрессионных моделей вида Y = F(X1 Х2,..., Хn), где Y - исследуемый показатель (объясняемая
переменная), а X1 Х2,..., Хn - объясняющие переменные (регрессоры). Как правило,
для построения таких моделей используются сети, обучаемые на массивах
статистических данных, отражающих наблюдаемую статистику зависимости переменной
Y от переменных X1 Х2,..., Хn (обучение с учителем). Основным преимуществом
нейронных сетей по сравнению с классическими методами регрессионного анализа
является принципиально более слабое требование к идентификации модели. В ходе
применения классических методов регрессионного анализа в ходе идентификации
модели необходимо достаточно точно указать вид искомой зависимости (например, Y
= а + b1Х1 +
b2Х2 +
…+ bnХn),
задаваемый набором параметров, и дальнейший анализ фактически сводится к оценке
значений этих параметров. Таким образом, в результате идентификации
регрессионной модели значительно сужается класс функций Y = F(X1 Х2,...,
Хn), в котором будет осуществляться поиск зависимости
наиболее согласующейся с данными наблюдений. Если модель идентифицирована
неверно, то исследуемый класс не будет содержать искомую зависимость, т.е.
последующий этап анализа будет заведомо обречен на неудачу. В отличие от
методов классического регрессионного анализа, идентификация нейронно-сетевой
модели состоит в выборе архитектуры нейронной сети, количества скрытых
нейронов, а также передаточных функций. В этом случае существенного сужения
исследуемого класса функций не происходит, поскольку класс зависимостей,
выражаемый нейронными сетями заданной архитектуры может быть весьма широким. В
частности, на основе знаменитой теоремы A.Н. Колмогорова [5] было установлено,
что любую непрерывную функцию f: [0,1]n ® [0,1] можно аппроксимировать при помощи трехслойной
нейронной сети, которая имеет n входных, 2n+1 скрытых и один выходной нейрон [2, с. 61]. Одним из
основных искомых свойств
нейронно-сетевой модели является ее обобщающая способность. Суть данного
свойства определяется на интуитивном уровне. Оно состоит в том, что сеть должна
показывать приблизительно одинаковые результаты на массиве данных, используемых
для обучения (обучающая выборка), и на массиве данных, которые отличаются от
обучающихся данных, но достаточно близких к ним (тестирующая, контрольная
выборки). Антиподом к сообщающему свойству нейронной сети является ее
неустойчивость, обусловленная переходом процесса обучения в режим запоминания
(memorize). Такая сеть демонстрирует минимальную ошибку на обучающем массиве
данных, но показывает высокий уровень ошибки при малых изменениях входных
данных. Математическим аналогом такого режима является подгонка статистических
данных полиномиальной зависимостью при условии, что степень полинома не
ограничена. Для любого набора входных векторов Х1, X2,
..., XN и выходных значений Y1,
Y2, ..., YN можно
подобрать полином Р(Х) достаточно высокой степени, такой, что для всех j = l,
2, ..., N будут верны точные равенства P(Xj)= Yj (нулевое
значение средней квадратической ошибки). При этом достаточно очевидно, что при
незначительных изменениях массива ошибка может быть очень большой. Переход
нейронной сети в режим запоминания, как правило, связан с «переопределенностью»
сети, обусловленной чрезвычайно большим числом скрытых нейронов и,
следовательно, большим количеством межнейронных соединений. В связи с этим
возникает задача, каким образом можно проводить оценку устойчивости
нейронно-сетевой модели и ее обобщающей способности. С математической точки
зрения устойчивость модели эквивалентна малым изменениям выходного параметра
при малых изменениях входных параметров. Таким образом, речь идет о выполнении
неравенства
|F(X) – F(X/)| ≤ A|X – X/|.
При этом оценка постоянной А может
считаться оценкой уровня устойчивости модели. Проблема заключается в следующем.
Для построения нейронно-сетевых регрессионных моделей, чаще всего используется
модель многослойного персептрона с гладкими передаточными функциями, а в
качестве алгоритма обучения используется алгоритм обратного распространения
ошибки (Back Propagation).
В этом случае при любых значениях весов
выходная функция нейронной сети Y = F(X1 Х2,..., Хn) является бесконечно дифференцируемой. Следовательно,
для любого компакта К в Rn
существует постоянная А(К), такая, что для X, X/ ÎК выполняется неравенство
|F(X)
– F(X/)| ≤ A(К)|X – X/|,
т.е. любая нейронная сеть с гладкими
передаточными функциями обладает
определенным уровнем устойчивости.
В связи
с этим, предлагается считать модель устойчивой, если ее уровень устойчивости
сравним с аналогичным уровнем устойчивости исходных данных,
использовавшихся для обучения сети. Смысл такого подхода состоит в
следующем. Обучение нейронной сети проводится на основе гипотезы, что
набор статистических данных (Xi,
Yi), где XiÎRn, представляет собой таблицу значений искомой
функции Y=F(X). Поскольку, процесс обучения сети состоит в нахождении функции,
наилучшим образом аппроксимирующей искомую зависимость, то оценивающая
зависимость (функция) должна обладать количественными характеристиками,
близкими к соответствующим характеристикам искомой функции. В частности,
уровень устойчивости оценивающей функции должен быть сравним с оценкой этого
уровня искомой функции. Оценку уровня устойчивости искомой функции можно получить на основе исходных данных.
Рассмотрим следующий алгоритм. Пусть (Xi,
Yi), i = 1,
2, …, N - таблица исходных
статистических данных. Для каждого фиксированного индекса i находим входной
вектор Хj,
ближайший к Хi относительно Евклидовой метрики:
|X i –X k| = |X i –X j|,
где |X i –X k| = 
.
Номер j зависит при этом от i, т.
е. j = j(i). Пусть 
= |X i –X j(i)|.
Положим Кi =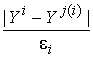 
(1)
Пусть
теперь Y = F(X) – нейронная сеть, обученная на
массиве данных (Xi, Yi), i = 1, 2, …, N. Введем в рассмотрение следующую
случайную величину, являющуюся сравнительной характеристикой устойчивости
исходных данных и нейронной сети. Для каждого i выберем случайный единичный вектор 
Rn. Положим
X i (
,
) = X
i + 
×
, 
,
.
Пусть далее 
= 
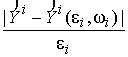(2)
Точки X i (
,
) и X j(i ) отстоят от точки X i на
равном расстоянии 
, поэтому величины Кi и 
, задаваемые соответственно
формулами (1) и (2), должны быть в каком-то смысле близки, т.е. их отношение
должно быть близко к 1. Тогда набор чисел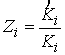 
можно считать набором
наблюдаемых значений случайной величины Z. Устойчивость нейронно-сетевой модели
Y=F(X) будем считать соответствующей устойчивости исходных данных, если
распределение случайной величины lnZ
близко к нормальному распределению с нулевым математическим ожиданием (т.е.
распределение величины Z является логнормальным). При этом возможна ситуация,
когда E(lnZ) 
0. Это означает, что нейронно-сетевая модель более устойчива,
чем исходные данные. В качестве обобщающего показателя сравнительной
устойчивости нейронно-сетевой модели может использоваться вероятность P(lnZ
< 0), т.е. вероятность того, что устойчивость модели будет не ниже, чем устойчивость исходных данных.
Таким образом, оценка соответствия уровня
устойчивости нейронно-сетевой модели должна проводиться по следующей схеме:
а) построение эмпирического распределения
величины lnZ;
б) Проверка гипотезы о нормальности
распределения величины lnZ;
в) Оценка вероятности Р(lnZ <0).
Литература:
1. Бойков И.В. Устойчивость нейронных сетей Хопфилда с запаздыванием // Известия высших учебных заведений. Поволжский регион. Физико-математические науки. – 2012. - №2(22). – с.85-97.
2. Головко В.А. Нейронные сети: обучение, организация и применение. Кн. 4: Учебное пособие для вузов / Общая ред. А.И. Галушкина. – М.: ИЖПР, 2001. – 256 с.
3. Иванов С.А. Область устойчивости в пространстве параметров рекурсивных нейронных сетей с топологией многомерного куба. Челябинск: Вестник ЮУрГУ серия Математика. Механика. Физика Выпуск 7, 2012.
4. Иванов С.А., Трум О.Н. Устойчивость нейронной сети со структурой связей в виде дерева [Электронный ресурс] – Режим доступа: http://www.rusnauka.com/4_SND_2013/Matemathics/4_126192.doc.htm
5.
Колмогоров А.Н. Представление непрерывных
функций многих переменных суперпозицией функций одной переменной и сложением //
Доклады АН СССР, 1958. - №5. – с.953 –956.