О решении задачи типа фильтрации
двухфазной несжимаемой и несмешивающейся жидкости
Б. С. Кабатаева, Хаджи Ахмад Джоя
Казахский национальный университет имени
аль-Фараби
Одной из важнейших задач повышения качества разработки
и рационального использования природных ресурсов нефтяных месторождений
является извлечение нефти. Поиск и реализация новых методов повышения
нефтеотдачи пластов является одним из важнейших направлений в нефтедобывающей
отрасли. При этом основными способами увеличения
дебита эксплуатационной скважины являются заводнение пластов или вытеснение
нефти оторочками из поверхностно-активных веществ, термическое воздействие,
система газлифта и т.д. Однако достичь полного извлечения нефти или газа не
удается. Это обусловлено рядом причин: сложностью поровой структуры пласта, его
неоднородностью, действием капиллярных сил, влиянием смачивающих свойств пород,
слагающих пласт и т.п.
Под фильтрацией понимают движение жидкостей в пористых
средах, т. е. твердых телах, пронизанных системами сообщающихся между собой
пустот (пор). В теории фильтрации принимается, что при выполнении ряда
естественных предположений о поровых системах после соответствующего
усреднения такие пористые среды и заполняющие их жидкости можно рассматривать
как сплошные среды [1]. Основной безразмерной характеристикой пористой среды
является пористость т(А), равная доле
объема пор в бесконечно малом элементе среды, содержащем фиксированную точку А. В связи с задачами проектирования и
эксплуатации нефтяных место рождений представляет большой интерес изучение
математических вопросов теории совместного движения в пористой среде двух
несмешивающихся несжимаемых жидкостей (например, нефти и воды) с плотностями ![]() и вязкостями
и вязкостями ![]() i=l , 2. Такое движение принято называть
двух фазной (или двухкомпонентной) фильтрацией . Главные характеристики
двухфазного фильтрационного движения — насыщенности
i=l , 2. Такое движение принято называть
двух фазной (или двухкомпонентной) фильтрацией . Главные характеристики
двухфазного фильтрационного движения — насыщенности ![]() и скорости фильтрации
и скорости фильтрации ![]() каждой жидкости в
точке А в момент времени t. Под насыщенностью
каждой жидкости в
точке А в момент времени t. Под насыщенностью ![]() понимается локальная доля порового пространства, занятого i-й
фазой. Заметим, что по определению
понимается локальная доля порового пространства, занятого i-й
фазой. Заметим, что по определению ![]() . Под скоростью фильтрации
. Под скоростью фильтрации ![]() понимают скорость
фиктивной жидкости, заполняющей всю среду, расход которой через любую площадку
совпадает с расходом i-и фазы реальной жидкости.
понимают скорость
фиктивной жидкости, заполняющей всю среду, расход которой через любую площадку
совпадает с расходом i-и фазы реальной жидкости.
Пусть дана (1)-(2) – задача Коши:
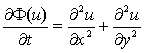 (1)
(1)
(1)
– Дифференциальное уравнение в частных производных
![]() (2)
(2)
(2)
– начальные условия.
Введем дополнительные условия, обеспечивающие
параболичность уравнения: ![]()
Преобразуем дифференциальное уравнение в частных
производных (1) в обыкновенное дифференциальное уравнение второго порядка
Введем безразмерную переменную
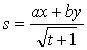 ,
,
где
![]() вещественные положительные постоянные, тогда
вещественные положительные постоянные, тогда ![]() .
.
Если ![]() , то
, то 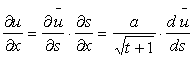
таким
образом
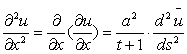
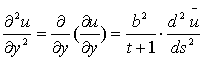
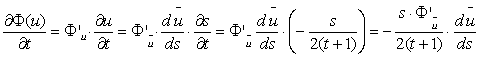
И,
следовательно, наше уравнение (1) будет выглядеть следующим образом:
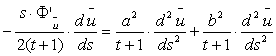
После
простых преобразований уравнение примет вид:
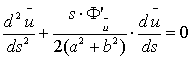 (3)
(3)
Таким образом, дифференциальное уравнение в частных производных (1) после
преобразований привели к виду обыкновенного дифференциального уравнения (3).
Рассмотрим краевые условия для уравнения (3). Для
начала краевые условия будем рассматривать на конечном отрезке ![]() , причем
, причем ![]() , затем будем расширять до
, затем будем расширять до ![]() :
:
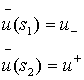 (4)
(4)
Применяя
обычные методы решения обыкновенных дифференциальных уравнений получаем решение
(3):
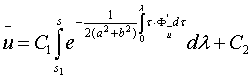 (5).
(5).
Используя
краевые условия (4) определим значения ![]() :
:
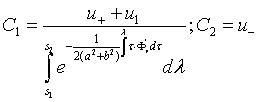
Введем
обозначение
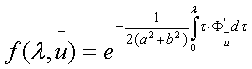
Тогда
решение краевой задачи (3)-(4) будет иметь вид:
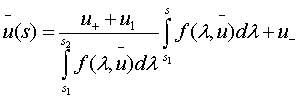
Введем
оператор ![]() такой что,
такой что,
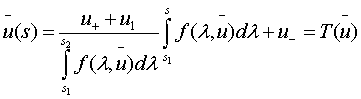
т.к.
![]() (данная функция является решением дифференциального уравнения
(3)) и решение уравнения определено для банаховых пространств, но для
Гильбертовых пространств может не всегда выполнятся, поэтому оператор
(данная функция является решением дифференциального уравнения
(3)) и решение уравнения определено для банаховых пространств, но для
Гильбертовых пространств может не всегда выполнятся, поэтому оператор ![]() - вполне непрерывный.
- вполне непрерывный.
![]() это означает, что для любой точки из промежутка
это означает, что для любой точки из промежутка ![]() ставится в
соответствие значение из этого промежутка
ставится в
соответствие значение из этого промежутка ![]() .
.
В
данном случае выполняется Теорема Шаудера о неподвижной точке.
Следовательно
задача имеет решение, т.е. решение существует.
Но
теорема Шаудера не выполняет условие единственности решения.
Единственность
решения можно рассмотреть следующим образом:
Пусть
задача (3)-(4) имеет два решения ![]() . И данные функции удовлетворяют краевым условиям (4).
. И данные функции удовлетворяют краевым условиям (4).
Пусть
существует еще одно решение данной задачи ![]() .
.
Но,
т.к. ![]() являются решениями
задачи (3)-(4), то они удовлетворяют краевым условиям (4). Следовательно,
являются решениями
задачи (3)-(4), то они удовлетворяют краевым условиям (4). Следовательно, ![]() . Т.е.
. Т.е. ![]() (*)
(*)
Из
теоремы Роля следует вывод, что внутри отрезка ![]() найдется точка
найдется точка ![]() в которой производная
в которой производная
![]() равно нулю. Также из
краевых условий (*) следует, что функция
равно нулю. Также из
краевых условий (*) следует, что функция ![]() равна нулю в точке
равна нулю в точке ![]() .
.
Далее
рассмотрим отрезки ![]() и
и ![]() . На этих отрезках также найдутся точки
. На этих отрезках также найдутся точки ![]() и
и ![]() соответственно, в
которых значение производной функции
соответственно, в
которых значение производной функции ![]() равно нулю. С учетом
(*) функция
равно нулю. С учетом
(*) функция ![]() равна нулю в данных
точках.
равна нулю в данных
точках.
Далее,
аппроксимируя данный процесс, приходим к выводу, что функция ![]() равна нулю в каждой
точке отрезка
равна нулю в каждой
точке отрезка ![]() .
.
Решение
задачи единственно.
Литература:
1.
Коновалов А.
Н. Задачи фильтрации многофазной несжимаемой жидкости. - Новосибирск: Наука,
1988. - 166 с.
1.2. Bahaerguli Nulahemaiti, Guo Jindong, Ж.Д. Байшемиров. О
некоторой постановке нестационарной
фильтраций жидкости в упруго-пористом
среде. Материалы международной конференции, Чехия – 2014. URL страницы: http://www.rusnauka.com/22_DNI_2014/Matemathics/4_174055.doc.htm
3.
Антонцев С.Н., Монахов В.Н. О некоторых задачах фильтрации двухфазной
несжимаемой жидкости // Динамика сплошной среды. 1969 г., Вып. 2.